Jika tidak ada kekuatan eksternal yang diterapkan pada sistem, sistem akan mengalami getaran bebas. Gerak sistem akan dibentuk oleh gangguan awal (kondisi awal).
Selain itu, jika tidak ada resistensi atau redaman dalam sistem, gerak osilasi akan terus selamanya dengan amplitudo konstan. Sistem seperti disebut undamped dan ditunjukkan pada gambar berikut,
Selain itu, jika tidak ada resistensi atau redaman dalam sistem, gerak osilasi akan terus selamanya dengan amplitudo konstan. Sistem seperti disebut undamped dan ditunjukkan pada gambar berikut,
Solusi untuk SDOF tidak teredam
Persamaan gerak diturunkan pada halaman pengantar dapat disederhanakan,
Dengan kondisi awal,
Persamaan gerak adalah perintah kedua homogen, persamaan diferensial biasa (ODE). Jika massa dan kekakuan pegas adalah konstanta, yang ODE menjadi ODE homogen linear dengan koefisien konstan dan dapat diselesaikan dengan metode Persamaan Karakteristik. Persamaan karakteristik untuk masalah ini adalah,
yang menentukan 2 akar independen untuk masalah getaran tidak teredam. Solusi akhir yang berisi 2 akar independen dari persamaan karakteristik dan memenuhi kondisi awal adalah,
Natural frequensi wn didefinisikan dengan,
dan hanya bergantung pada massa sistem dan kekakuan pegas (yaitu setiap redaman tidak akan mengubah frekuensi alami sistem).
Atau, solusinya dapat dinyatakan dengan bentuk yang setara,
Dimana amplitudo A0 dan fase awal f0,
Contoh Perilaku Waktu
Perpindahan dari sistem tak teredam akan muncul sebagai berikut,
Harap dicatat bahwa asumsi redaman nol biasanya tidak akurat. Pada kenyataannya, ada hampir selalu ada beberapa hambatan dalam sistem getaran. Perlawanan ini akan lembab getaran dan menghilangkan energi; gerakan osilasi yang disebabkan oleh gangguan awal pada akhirnya akan berkurang menjadi nol.








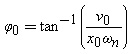

Tidak ada komentar:
Posting Komentar